Análisis Factorial Confirmatorio

FACULTAD DE CIENCIAS SOCIALES - PUCP
Curso: POL 304 - Estadística para el análisis político 2 | Semestre 2024 - 2
Jefas de Práctica: Karina Alcántara 👩🏫 y Lizette Crispín 👩🏫
Vamos a trabajar con una base de datos creada por unos alumnos que buscan poder explicar la variable de desigualdad de género a nivel de países. Esta base de datos tiene las siguientes variables independientes:
País: País del que pertenece la información
DesigualdadGenero: Indice de desigualdad de género
MLAutonomia: Mide que tanto el sistema legal protege derechos reproductivos de las mujeres
MLViolencia: Mide que tanto el sistema legal protege a las mujeres de la violencia
VozPolítica: Presencia de mujeres en el parlamento
LibertadMov: Porcentaje de mujeres que declaran no sentirse seguras en las calles
DesconfianzaSJ: Porcentaje de mujeres que no confian en el sistema de justicia
SecundariaC: Porcentaje de población con secundaria completa
DesempleoMuj: Ratio de desempleo de mujeres frente a hombres
CuentaF: Porcentaje de mujeres que cuentan con una cuenta en el sistema financiero.
Las dos primeras variables son descriptivas, la primera es con respecto al país y la segunda es el índice, como un resultado final.
Lo llamaremos subdata:
Paso 1: Matriz de correlaciones
Generamos la matriz de correlaciones para identificar qué variables de nuestra subdata están correlacionadas.
library(psych)
cor.plot(corMatrix,
numbers=T, #Se muestren los numeros de las correlaciones
upper=F, #Que aparezca la segunda parte
main= "Matriz de correlaciones",#Titulo
show.legend=T)#Mostrar leyenda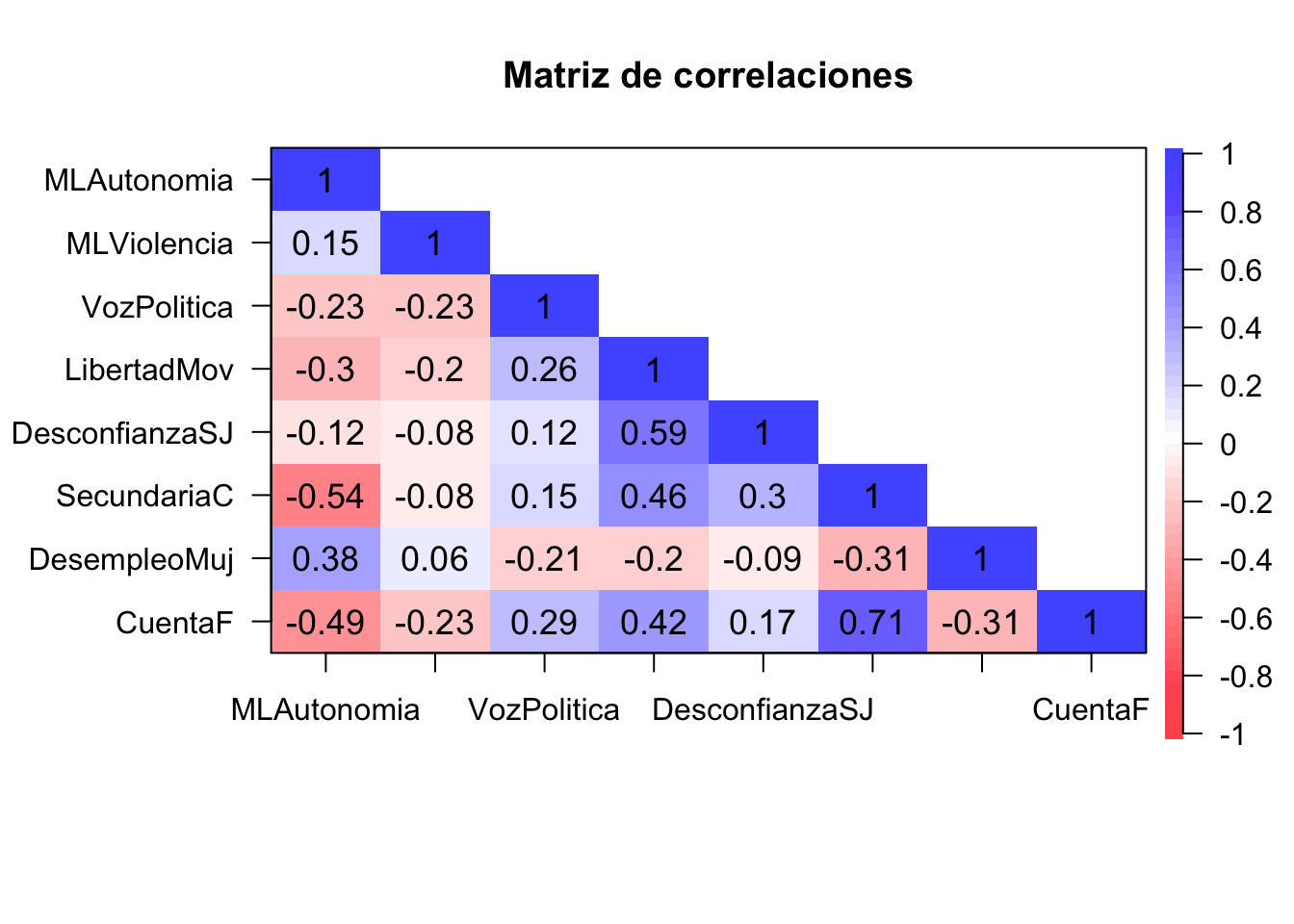
Paso 2: Corroborar si se puede factorizar
KMO
Proceso correlación
## Kaiser-Meyer-Olkin factor adequacy
## Call: psych::KMO(r = subdata)
## Overall MSA = 0.73
## MSA for each item =
## MLAutonomia MLViolencia VozPolitica LibertadMov DesconfianzaSJ
## 0.83 0.66 0.75 0.73 0.60
## SecundariaC DesempleoMuj CuentaF
## 0.70 0.85 0.72Bartlet
cortest.bartlett(corMatrix,n=nrow(subdata))$p.value>0.05 #Menor a 0.05 saldrá FALSE, mayor a 0.05 saldra TRUE## [1] FALSEPaso 3: Análisis Factorial Exploratorio
Gráfico de sedimentación
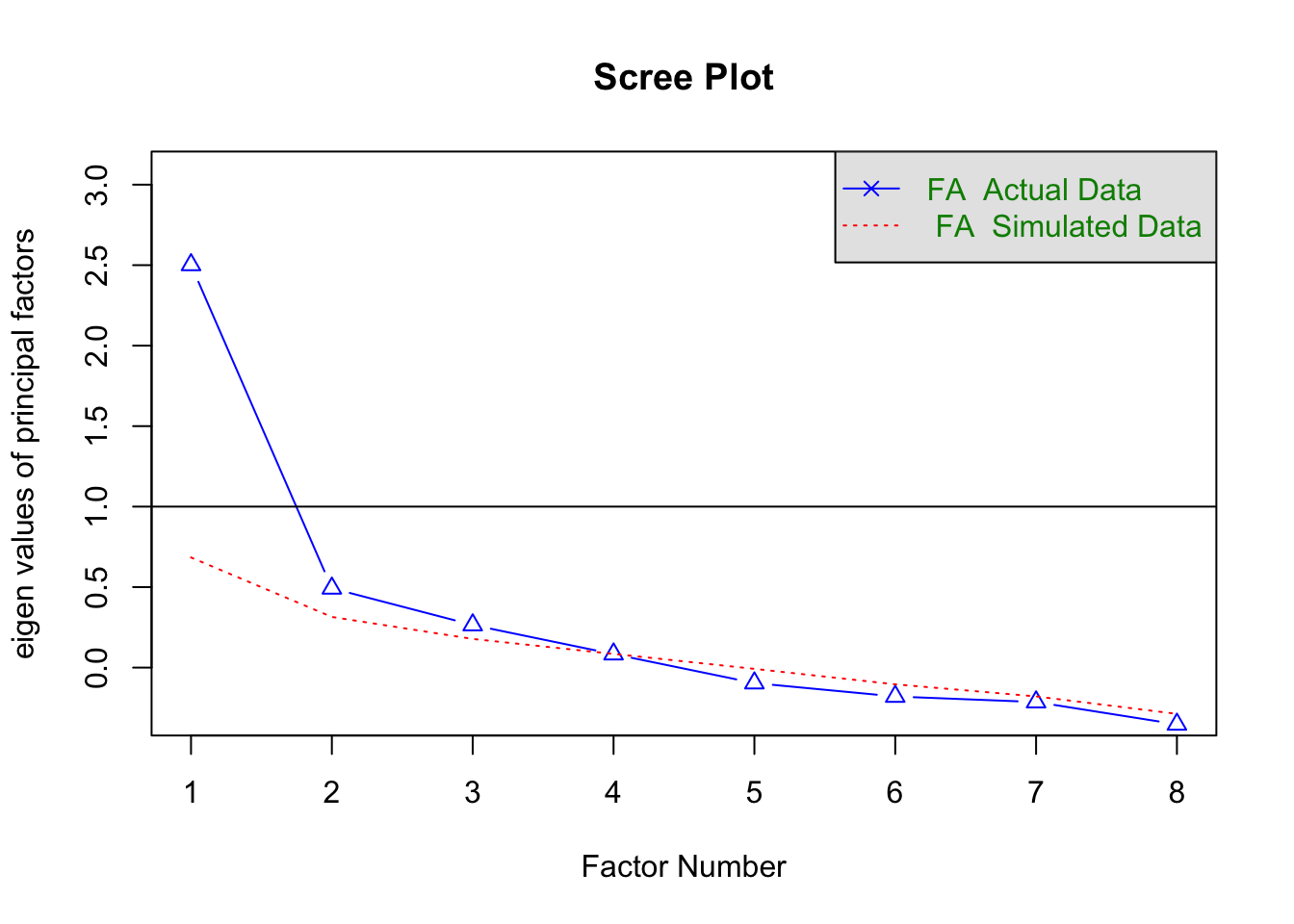
## Parallel analysis suggests that the number of factors = 3 and the number of components = NAAutovalores
## [1] 3.0714888 1.2071756 1.0772113 0.8265806 0.7015968 0.5154084 0.3600658
## [8] 0.2404727También recomienda 3 factores :)
Factorizar
## Factor Analysis using method = minres
## Call: fa(r = subdata, nfactors = 3, rotate = "varimax", fm = "minres")
## Standardized loadings (pattern matrix) based upon correlation matrix
## MR1 MR2 MR3 h2 u2 com
## MLAutonomia -0.58 -0.06 -0.31 0.44 0.5576 1.6
## MLViolencia -0.08 -0.09 -0.37 0.15 0.8504 1.2
## VozPolitica 0.15 0.10 0.51 0.30 0.7048 1.3
## LibertadMov 0.26 0.77 0.30 0.75 0.2466 1.5
## DesconfianzaSJ 0.08 0.71 0.06 0.51 0.4877 1.0
## SecundariaC 0.94 0.32 -0.07 1.00 0.0035 1.2
## DesempleoMuj -0.36 -0.03 -0.27 0.21 0.7941 1.9
## CuentaF 0.70 0.17 0.32 0.61 0.3863 1.5
##
## MR1 MR2 MR3
## SS loadings 1.95 1.25 0.77
## Proportion Var 0.24 0.16 0.10
## Cumulative Var 0.24 0.40 0.50
## Proportion Explained 0.49 0.32 0.19
## Cumulative Proportion 0.49 0.81 1.00
##
## Mean item complexity = 1.4
## Test of the hypothesis that 3 factors are sufficient.
##
## The degrees of freedom for the null model are 28 and the objective function was 2.27 with Chi Square of 264.39
## The degrees of freedom for the model are 7 and the objective function was 0.05
##
## The root mean square of the residuals (RMSR) is 0.03
## The df corrected root mean square of the residuals is 0.05
##
## The harmonic number of observations is 121 with the empirical chi square 4.49 with prob < 0.72
## The total number of observations was 121 with Likelihood Chi Square = 6.28 with prob < 0.51
##
## Tucker Lewis Index of factoring reliability = 1.012
## RMSEA index = 0 and the 90 % confidence intervals are 0 0.105
## BIC = -27.29
## Fit based upon off diagonal values = 0.99
## Measures of factor score adequacy
## MR1 MR2 MR3
## Correlation of (regression) scores with factors 0.98 0.86 0.78
## Multiple R square of scores with factors 0.96 0.74 0.61
## Minimum correlation of possible factor scores 0.92 0.47 0.21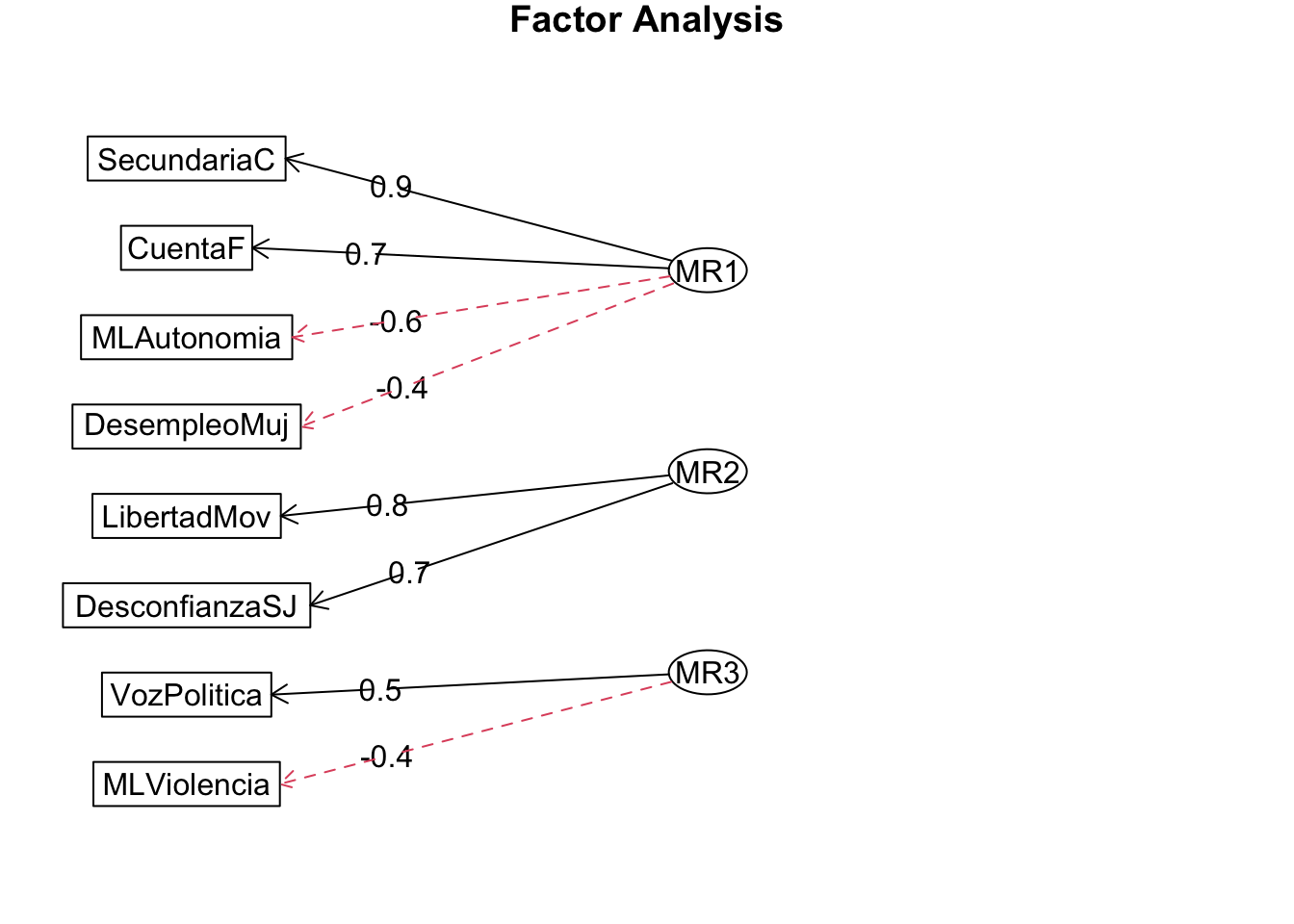
Podemos observar que hay unas líneas punteadas rojas, ello implica que las cargas factoriales son negativas, lo que significa que la relación entre la variable observable y el factor creado es inversa.
** Vemos cargas factoriales y cumulative var.**
##
## Loadings:
## MR1 MR2 MR3
## MLAutonomia -0.585 -0.311
## MLViolencia -0.368
## VozPolitica 0.512
## LibertadMov 0.259 0.773 0.298
## DesconfianzaSJ 0.708
## SecundariaC 0.943 0.319
## DesempleoMuj -0.363 -0.271
## CuentaF 0.696 0.318
##
## MR1 MR2 MR3
## SS loadings 1.951 1.251 0.767
## Proportion Var 0.244 0.156 0.096
## Cumulative Var 0.244 0.400 0.4961.Ver qué variables tiene cada componente
2.Ver la carga, que tanto aporta cada variable al componente.
3.Proportion Var y Cumulative Var
Paso 4: Análisis Factorial confirmatorio
Como tenemos una sugerencia planteada en el AFE, lo corroboraremos con el AFC.
En caso una variable observable comparte en más de un factor la consideraremos en donde tiene una mayor carga factorial.
## [1] "MLAutonomia" "MLViolencia" "VozPolitica" "LibertadMov"
## [5] "DesconfianzaSJ" "SecundariaC" "DesempleoMuj" "CuentaF"Modelo_confir <- "FAC1 =~ SecundariaC + CuentaF + MLAutonomia + DesempleoMuj
FAC2 =~ LibertadMov + DesconfianzaSJ
FAC3 =~ VozPolitica + MLViolencia"
Modelo_confir## [1] "FAC1 =~ SecundariaC + CuentaF + MLAutonomia + DesempleoMuj\n FAC2 =~ LibertadMov + DesconfianzaSJ\n FAC3 =~ VozPolitica + MLViolencia"Lo que se realizaría es indicar el nombre de cada facrtor, y qué variables las integran, solo indicamos el nombre de estas variables, en el siguiente comando indicaríamos la base
## lavaan 0.6.16 ended normally after 255 iterations
##
## Estimator ML
## Optimization method NLMINB
## Number of model parameters 19
##
## Number of observations 121
##
## Model Test User Model:
##
## Test statistic 23.470
## Degrees of freedom 17
## P-value (Chi-square) 0.135
##
## Parameter Estimates:
##
## Standard errors Standard
## Information Expected
## Information saturated (h1) model Structured
##
## Latent Variables:
## Estimate Std.Err z-value P(>|z|)
## FAC1 =~
## SecundariaC 1.000
## CuentaF 0.941 0.106 8.902 0.000
## MLAutonomia -0.009 0.001 -6.895 0.000
## DesempleoMuj -0.006 0.001 -4.197 0.000
## FAC2 =~
## LibertadMov 1.000
## DesconfianzaSJ 0.388 0.110 3.533 0.000
## FAC3 =~
## VozPolitica 1.000
## MLViolencia -0.013 0.006 -2.185 0.029
##
## Covariances:
## Estimate Std.Err z-value P(>|z|)
## FAC1 ~~
## FAC2 138.009 30.184 4.572 0.000
## FAC3 78.279 29.080 2.692 0.007
## FAC2 ~~
## FAC3 31.992 11.128 2.875 0.004
##
## Variances:
## Estimate Std.Err z-value P(>|z|)
## .SecundariaC 251.725 62.639 4.019 0.000
## .CuentaF 261.953 58.521 4.476 0.000
## .MLAutonomia 0.075 0.011 6.900 0.000
## .DesempleoMuj 0.128 0.017 7.529 0.000
## .LibertadMov -16.010 31.116 -0.515 0.607
## .DesconfianzaSJ 43.848 7.328 5.984 0.000
## .VozPolitica 91.391 23.388 3.908 0.000
## .MLViolencia 0.036 0.006 6.195 0.000
## FAC1 644.026 122.846 5.243 0.000
## FAC2 126.940 34.105 3.722 0.000
## FAC3 41.112 23.687 1.736 0.083Nos fijamos en la tabla de Latent Variables, y que las variables tengan un pvalue menor a 0.05 para concluir que si aportan a los factores de manera significativa.
Graficamos
semPaths(modelo, intercepts = FALSE,edge.label.cex=1.5, optimizeLatRes = TRUE, groups = "lat",pastel = TRUE, exoVar = FALSE, sizeInt=5,edge.color ="black",esize = 6, label.prop=2,sizeLat = 6,"std", layout="circle2")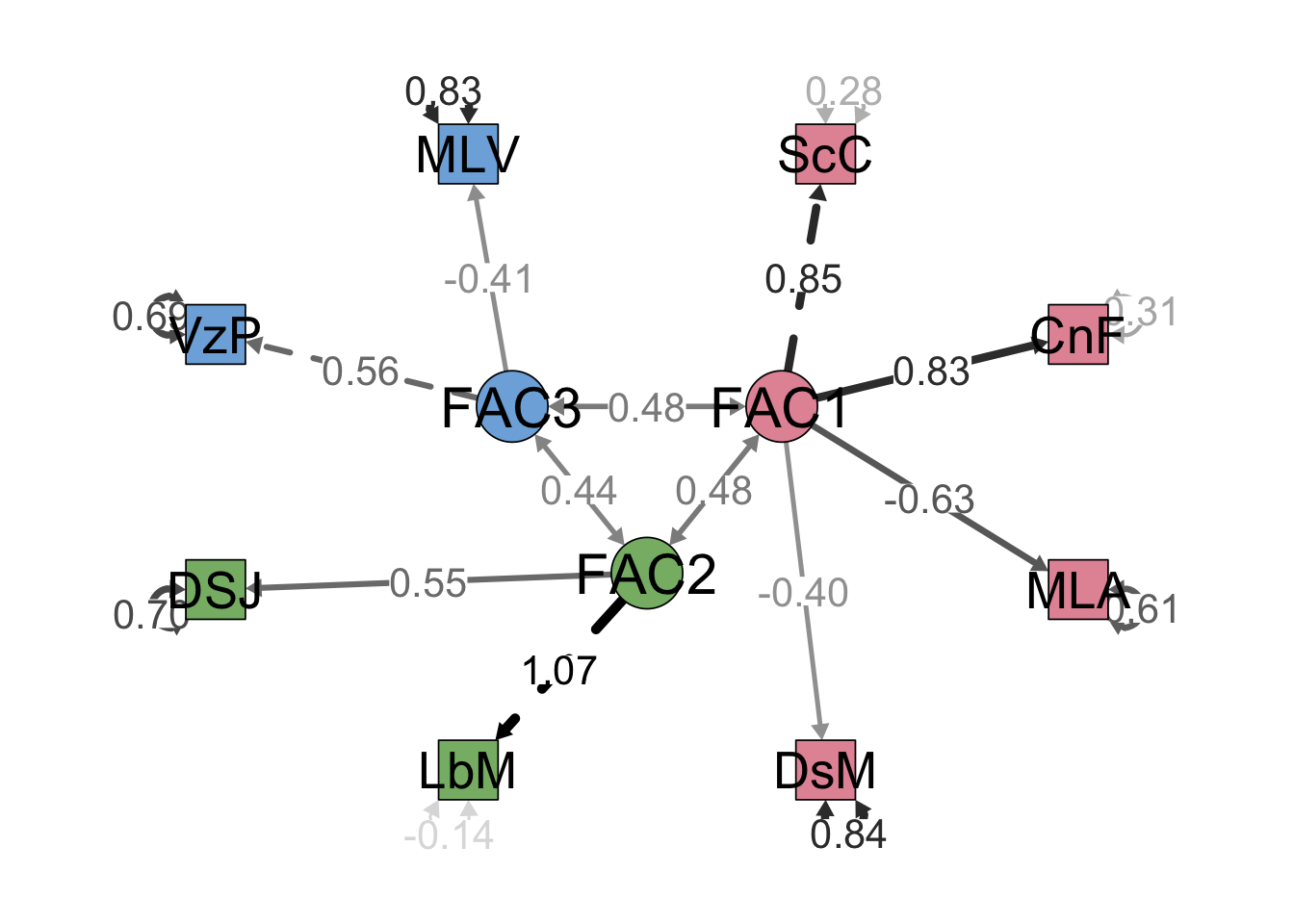
Podemos observar los 3 factores creados. Los numeros que vemos entre los factores y las variables latentes son las cargas facrtoriales, mientras más fuerte la línea o número mayor carga factorial tendrá. los numeros que vemos direccionados hacia las variable observable es la información que no es eplicada con el factor, lo esperado es que este sea menor que la carga factorial.
Agregamos los factores del AFC a la base de datos
library(BBmisc)
data$autoecon <- normalize(puntajes_factores$FAC1,
method = "range",
margin=2, # by column
range = c(0, 10))
data$percpinst <- normalize(puntajes_factores$FAC2,
method = "range",
margin=2, # by column
range = c(0, 10))
data$autopol <- normalize(puntajes_factores$FAC3,
method = "range",
margin=2, # by column
range = c(0, 10))## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 2.754 5.311 5.272 7.745 10.000## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 4.410 5.644 5.430 6.584 10.000## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 0.000 3.701 4.936 4.936 6.139 10.000